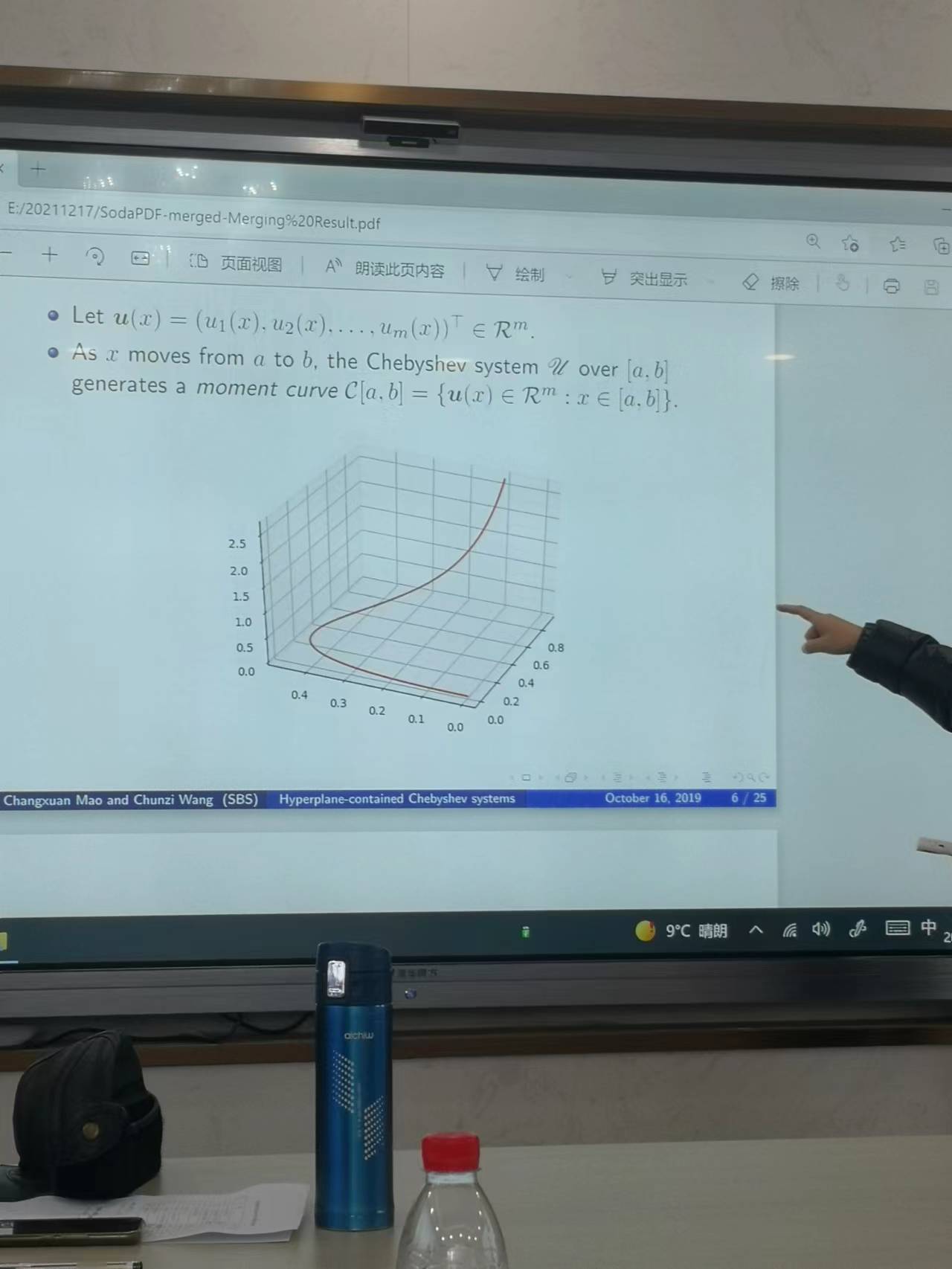
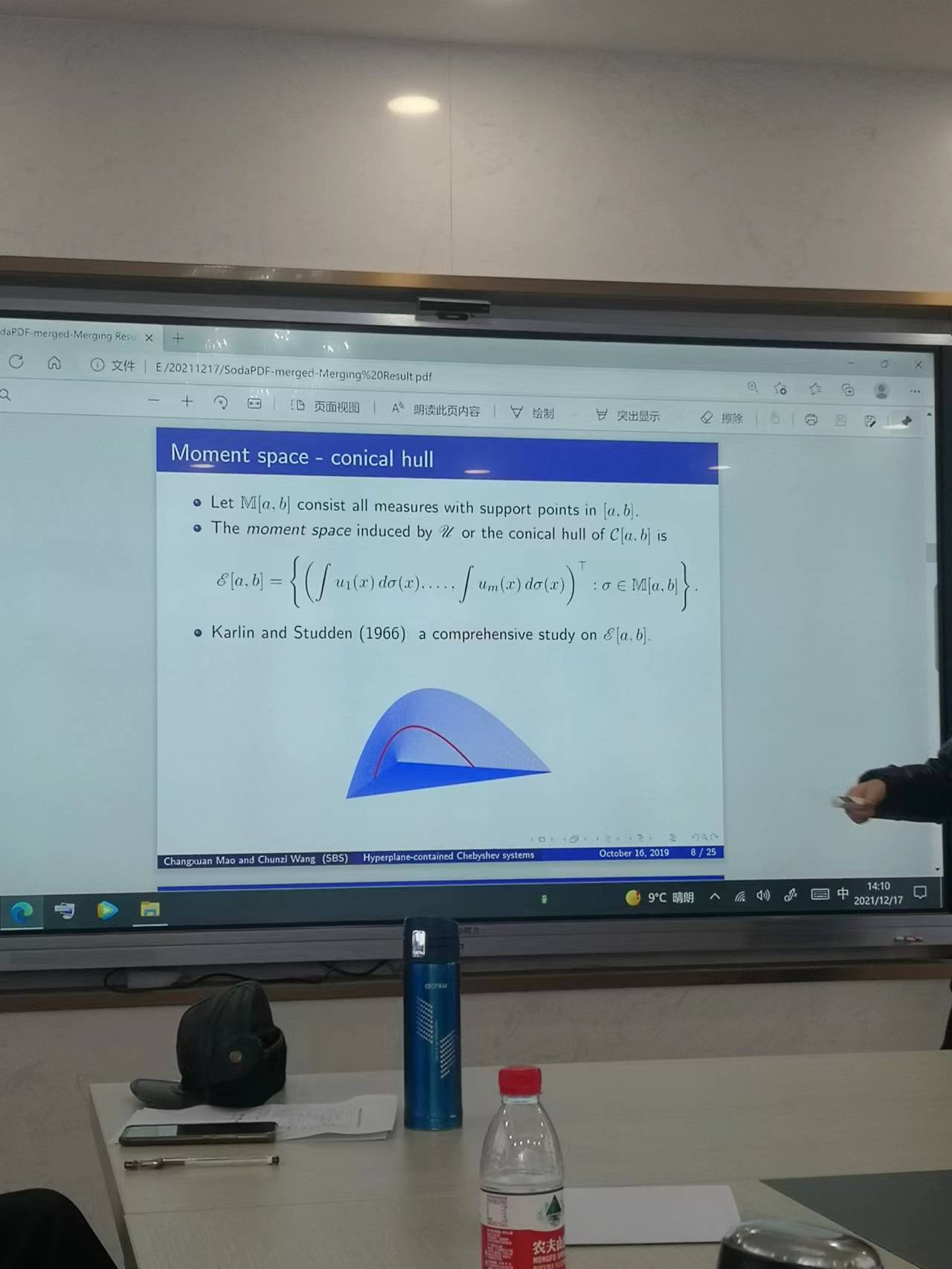
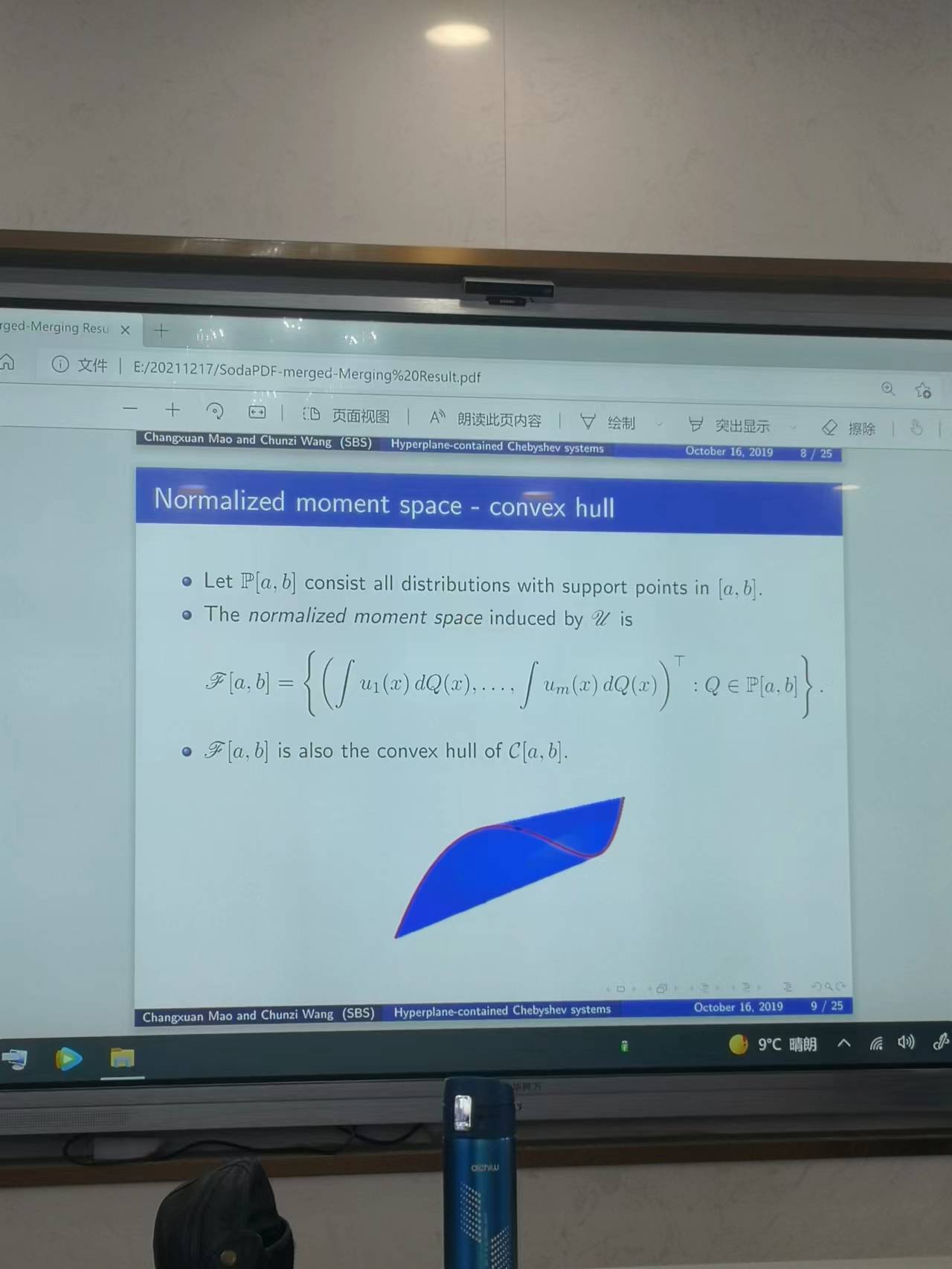
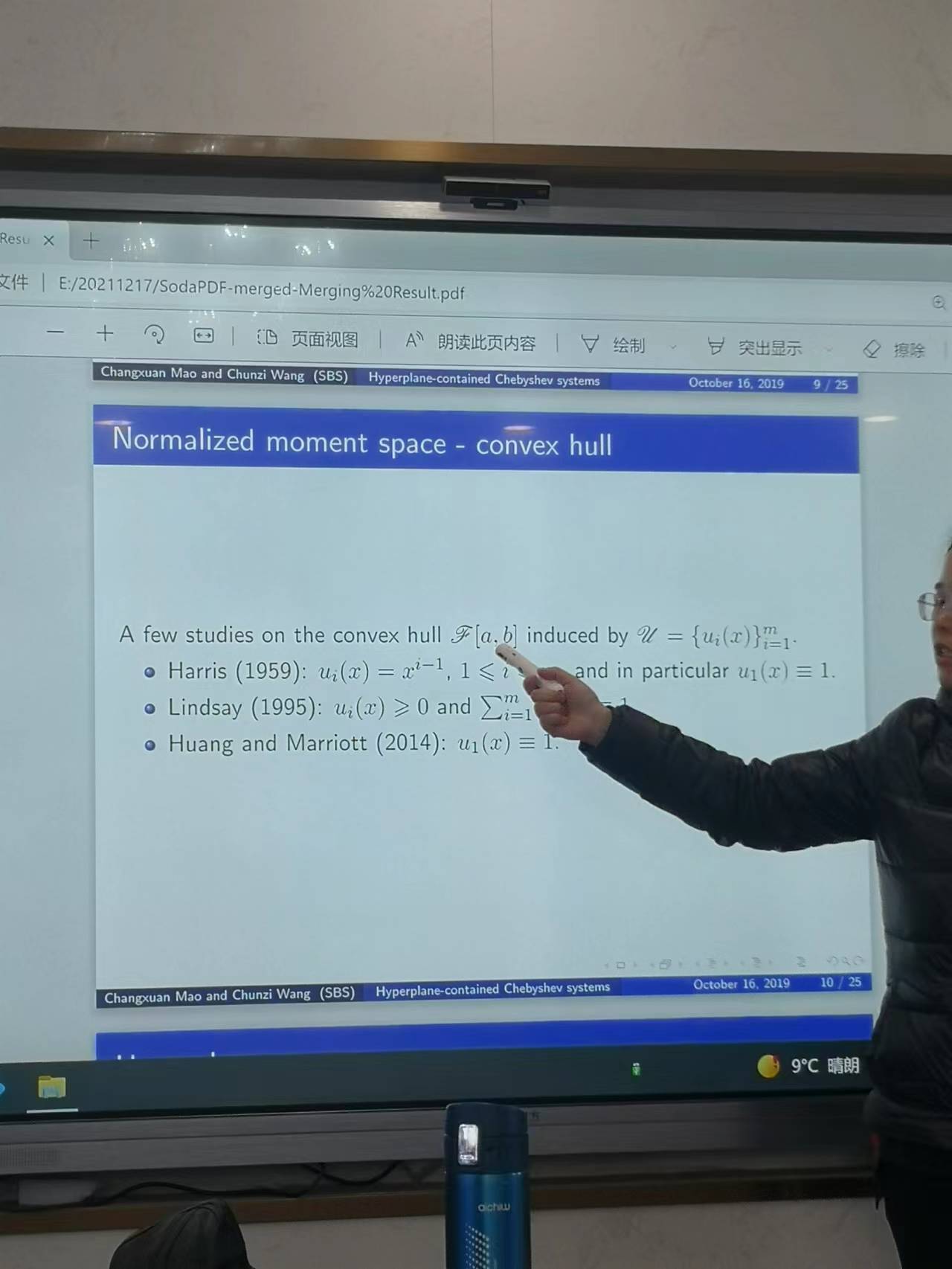
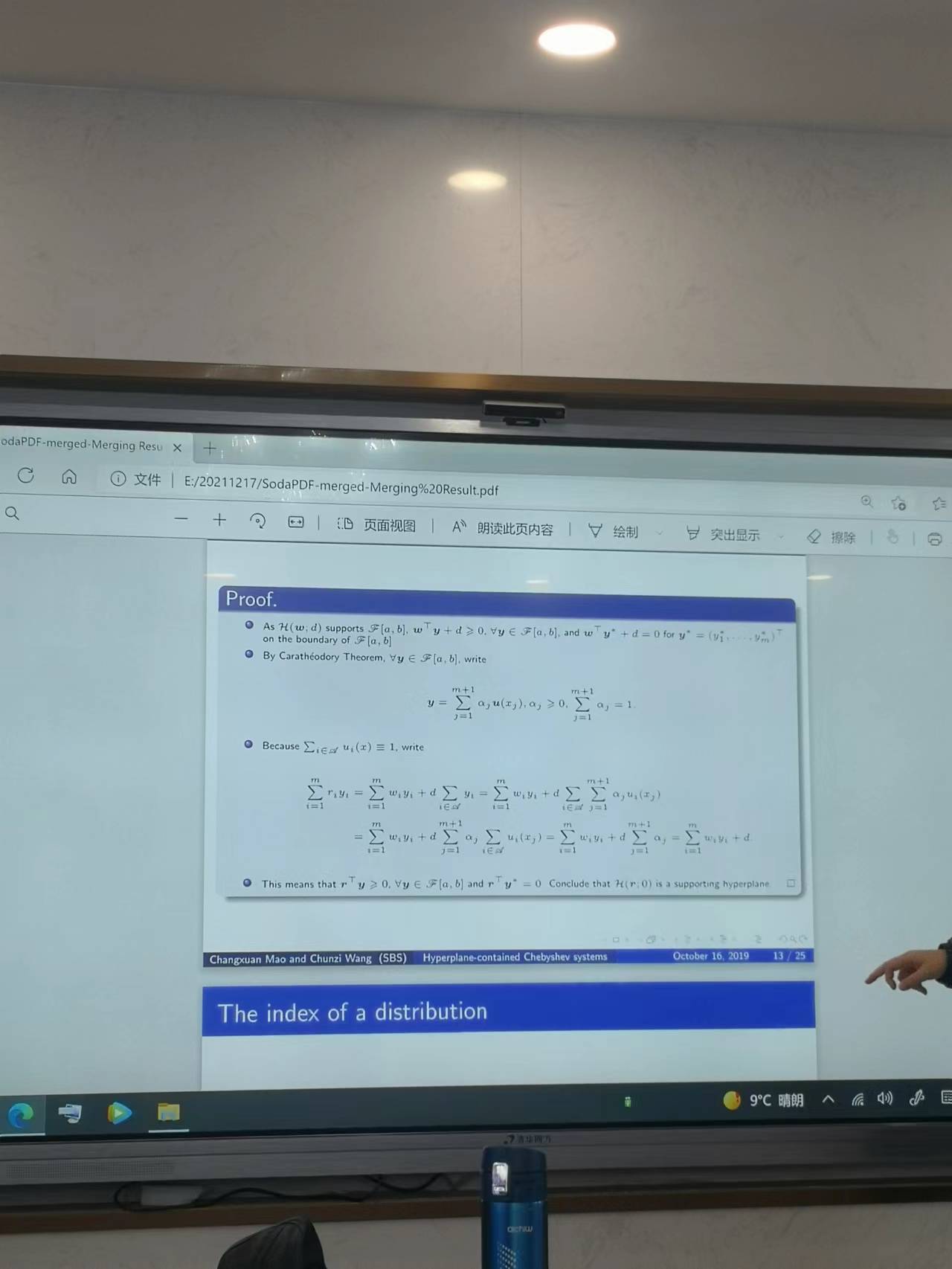
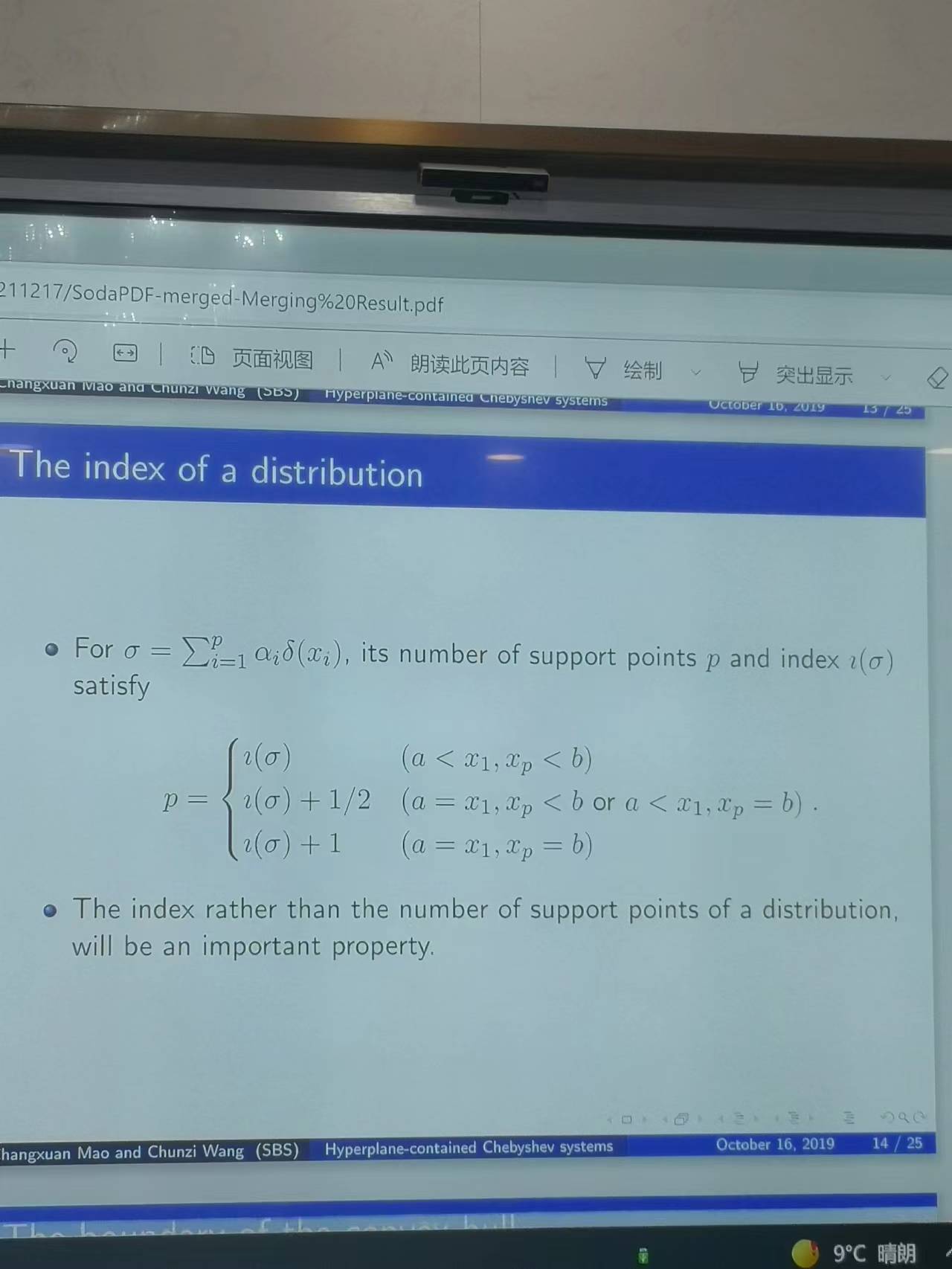
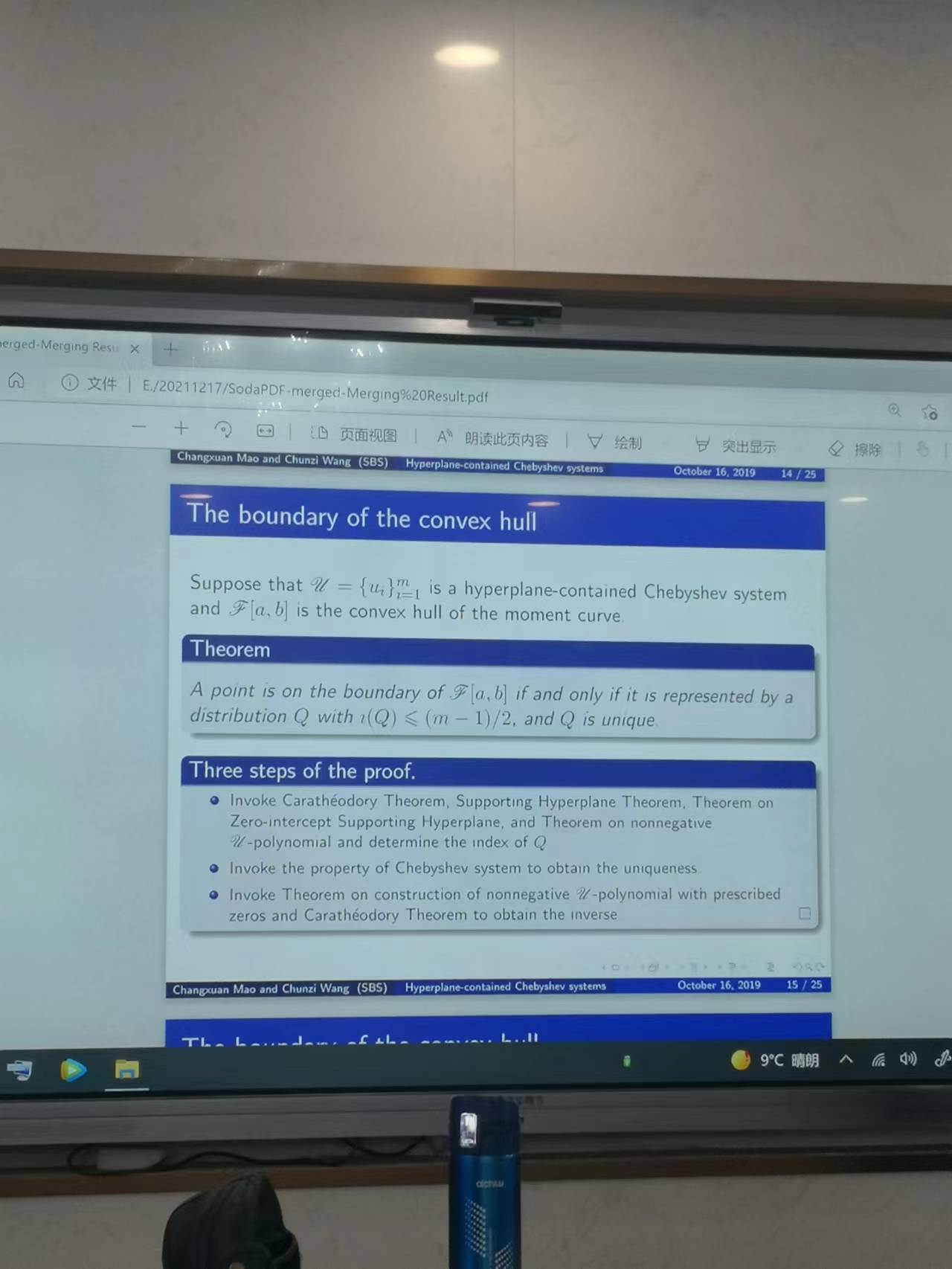
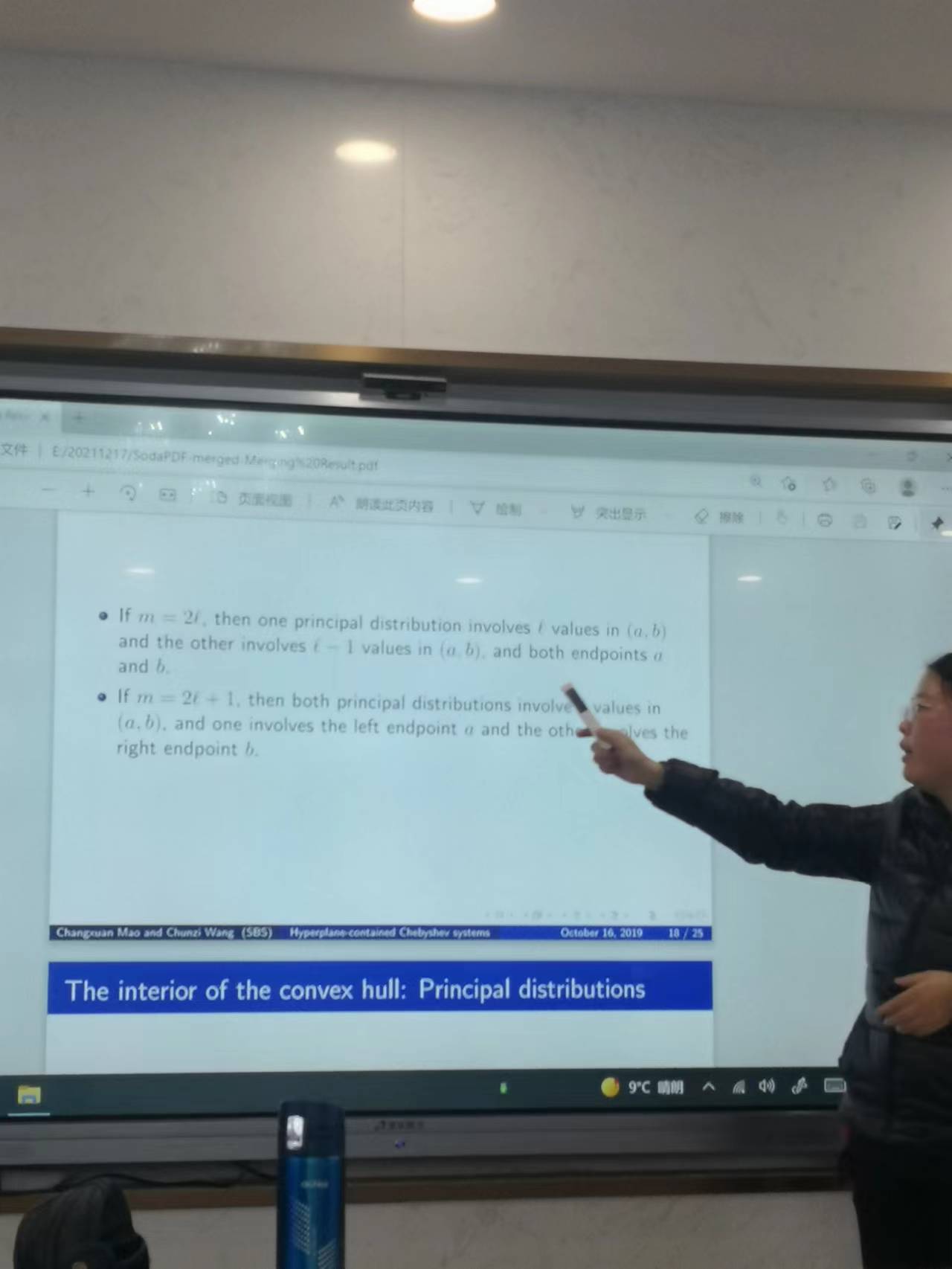
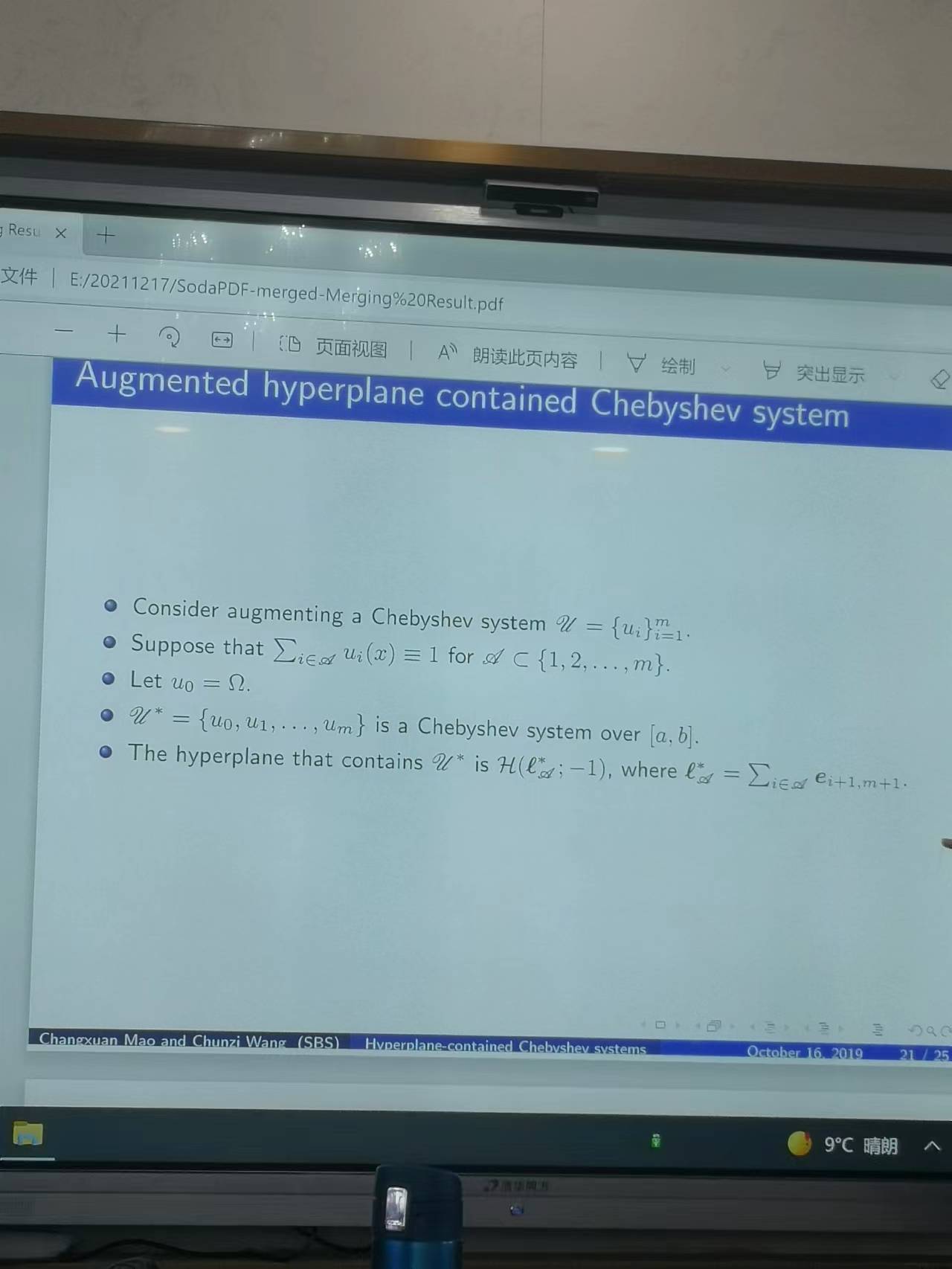
2021年12月17日👐🏻，王春子老師給万达平台教師作了題為《密度切比雪夫系統的拓展與應用》的講座。王春子老師的講座分為五個部分，分別是切比雪夫系統和廣義多項式、矩曲線和凸分析問題、超平面問題🙍🏼‍♂️、凸包的邊界問題和內部問題，一個具有修正的切比雪夫優化算法。在講座開始，王春子老師首先介紹了切比雪夫系統和廣義多項式問題，在一個閉區間上存在著連續函數，若在閉區間上不恒為零的線性多項式至多有m-1個零點，那麽函數組就是一個切比雪夫系統👮🏽🤵🏻‍♀️。隨後王老師又對廣義多項式進行了說明，如果連續函數的線性多項式最多有m-1個零點，那麽其線性表達式即為廣義多項式。在限定了x的表達式後🤹‍♂️，對該切比雪夫系統擬合了力矩曲線。隨後🏌🏼‍♂️，王老師就力矩空間中的錐殼問題、歸一化矩空間的凸包問題進行了相關的拓展。在其間，王春子老師引出了超平面問題。王春子老師還就凸包的邊界問題進行了闡述，假如有一個點在力矩曲線的凸包上，那麽其分布就是唯一的🧝‍♀️📳，王老師在講解該問題的時候給出了簡要的證明🩰。那麽🤯，在凸包的內部又是如何的情況呢，王老師就該問題也進行了簡要的證明，在凸包的內部，有大致兩個分布，且該分布的支撐點互相交織🤹🏼‍♂️。在講座的最後，王老師就切比雪夫系統的改進超平面進行了相應的闡釋。並使用之前所講到的相關的問題就最優化問題進行了例證。王老師所講述的相關問題在某些領域是非常重要的，比如在工程學問題、時變的時間序列以及其他問題上都有可能會有應用和突破。相信王老師給我們做的講座是能夠給我們帶來更好的視野👩🏿‍🎤⛹🏼‍♂️，兼具更好的拓展性的，對於王老師來說，這可能僅僅是她的開始🧑🏽‍🦳，希望她能夠給我們帶來更多的學術前沿的分享。

（供稿：曹煥）